1. Introduction
1.1 Introducing the Scheming Slave (servus callidus)
To trick or to be tricked seems to be one of the central questions of Roman comedy. Intrigue is the order of the day, with many characters plotting against each other. In this paper, I will examine the data trends for the scheming characters in Roman comedy. Here the role of the schemer is closely linked to that of the male slave as many plots, intrigues, and deceptions are initiated by a cunning slave, a servus callidus. In fact, he is one of the most prominent character types of Roman comedy. This character usually comes into play when a young man finds himself in a hopeless situation, for example when his father or rivals threaten to destroy his affair with a young girl or prostitute. The man of the moment who helps the hopeless young man is the servus callidus. All the young man has to do is step back and let his slave plot against his opponents. The latter is sometimes more, sometimes less successful in his intrigues. In my analysis, I focus on this type of schemer and aim to create a data profile of the scheming slave (servus callidus).
This article is aimed at both scholars of Roman comedy and researchers in the digital humanities. It will demonstrate the value of applying network analysis to Roman comedy, especially by providing new insights into the servus callidus and contributing to our understanding of this character type. For digital humanists, this study can serve as a use case for literary network analysis of a comparatively small corpus of texts.
1.2 Introducing Dramatic Networks and Network Measures
Using sociological methods, we can analyse the scheming slave as part of a social network within the respective drama.1 Since the servus callidus is a character type of Roman comedy, he is likely to hold a specific position in the social network of a drama. We can therefore expect certain data trends to emerge for the scheming slaves when analysing the dramatic networks. The method of network analysis promises a new perspective on the scheming slave as it allows us to quantify the social capital of this character type.
Social capital
Several scholars have attempted to capture the characteristics of social networks mathematically and in particular to approach the phenomenon of social capital. Bourdieu defines social capital as follows: “Social capital is the aggregate of the actual or potential resources which are linked to possession of a durable network of more or less institutionalized relationships of mutual acquaintance and recognition – or in other words, to membership in a group.” (Bourdieu 1986, 248). An important aspect is highlighted here: Social capital is based not only on actual but also on potential network resources.
In the case of the servus callidus, not all relationships per se give him access to the resources of another character; his social capital is thus dependent on others.2 Through his intrigues, he tries to gain access to material capital, such as the property of the head of the family, the paterfamilias. Moreover, according to Bourdieu, social capital can be transformed into other types of capital (Bourdieu 1986, 252–55). This transformation process of social capital is the focus of the actions of the servus callidus who uses social relations primarily to gain material possessions.3
Network measures
Bourdieu’s concept of social capital has been further elaborated.4 Some scholars have developed network measures to operationalise social capital on the micro, meso, or macro level (Jansen and Diaz-Bone 2011, 85–86). For this paper, I am particularly interested in the centrality measures. The centrality measures are designed to identify central, hence important social actors within the network and thus focus on the micro level.5 They can, therefore, provide important insights into the characteristics of the servus callidus. Each type of centrality is based on a specific differentiated theoretical model of social capital and the resulting resources. The degree centrality, for example, assumes that social capital means having relations to many different social actors whereas the weighted degree centrality highlights the frequency of interactions in these relationships as being essential for social capital. The closeness centrality, on the other hand, regards social capital as being in close proximity to other actors in the social network. For my analysis, I consider the aforementioned measures, namely the degree centrality, weighted degree centrality, and closeness centrality.6 I also analyse the betweenness centrality,7 which I will explain in subsection 2.1 of this article.8
Regarding the role of the schemer, I also analyse the clustering coefficient as it indicates whether a character can more easily play other characters against each other.9 The calculation takes into account the number of triangles of a character, i.e., the number of groups of three a character is part of. To contextualise these character-specific values, I also consider general network values, the average degree centrality and the average clustering coefficient.
1.3 Introducing Count-Based Measures
For the analysis of the schemer, I also examine count-based measures, namely the number of words spoken by a character, the number of speech acts, and the number of scenes in which the character appears. The greater the number, the greater the presence of the character in the play. Moreover, a large number might imply that a character dominates the action of the play.
2. Hypotheses for Analysing Schemers with Digital Methods
2.1 Exploring Schemers through Network Analysis
Certain positions within a network make it possible to influence the network in a certain way. In this respect, the betweenness centrality is particularly important when analysing schemers. The betweenness centrality shows how often a node or character is part of the shortest path between other nodes or characters. A high betweenness centrality indicates that the respective node or character can access information faster than others in the network. It can therefore influence the flow of information and act as a broker (Fuhse 2018, 60–62). Such a position could be very advantageous for a schemer. However, the betweenness centrality signifies only the potential to control the flow of information.10 Whether a character realises its potential as a broker should be examined case by case.
The clustering coefficient is another measure of increasing importance for the analysis of schemers. This measure gives the number of connections between the neighbours of a node. The calculation takes into account the number of triangles of a node. A low clustering coefficient marks characters that can turn two other characters against each other more easily (Fuhse 2018, 22, 167). For instance, if character A and character B do not interact directly, but both interact with character C, it is easier for character C to play character A against character B and vice versa. In a network that consists only of character A, character B, and character C, the clustering coefficient of character C is 0 because its two neighbours do not interact. Furthermore, as character A and character B only have one relationship each and at least two neighbours are required to calculate the clustering coefficient, a clustering coefficient is not available for character A and character B.
Following these definitions, a character with a high betweenness centrality and a low clustering coefficient can act as a broker and as a manipulator. In such a position, the character can exercise power over other characters.11 Both values thus indicate which characters have potentially powerful and advantageous positions within the dramatic network. The following network effects are likely to constitute the social capital of the servus callidus and are indicated by specific network measures: access to information (indication: high betweenness centrality) and power (indication: high betweenness centrality, low clustering coefficient).12 The servus callidus should therefore have a high betweenness centrality and a low clustering coefficient. While it is advantageous for a schemer if his victims do not interact (indication: low clustering coefficient), he himself is likely to interact with many different characters. This would result in a large number of triangles.
A high degree centrality, and even more a high weighted degree centrality, characterises those characters who verbally interact most with other characters. Furthermore, the centralisation on one character (indication: high centralities) gives this character a coordinating role in the network (Fuhse 2018, 170), which would also favour intrigues. Accordingly, the type of the servus callidus should have high centralities.
These considerations lead to the following partially graded hypotheses for the analysis:
1. In the respective network, the degree centrality, weighted degree centrality, closeness centrality, and betweenness centrality of the schemer are the highest values.
2. In the respective network, the degree centrality, weighted degree centrality, closeness centrality, and betweenness centrality of the schemer are among the three highest values.
3. In the respective network, the degree centrality of the schemer is above average.
4. In the respective network, the clustering coefficient of the schemer is the lowest value while the number of triangles is the largest value.
5. In the respective network, the clustering coefficient of the schemer is among the three lowest values while the number of triangles is among the three largest values.
6. In the respective network, the clustering coefficient of the schemer is below average.
7. In the respective network, the betweenness centrality of the schemer is the highest value while the clustering coefficient is the lowest value.
8. In the respective network, the betweenness centrality of the schemer is at least the third highest value while the clustering coefficient is at least the third lowest value.
2.2 Exploring Schemers through Count-Based Measures
To sharpen this profile, we can consider count-based measures, namely the number of words spoken by the schemer, the number of his speech acts, and the number of scenes which feature a schemer. Since the cunning slave usually controls large parts of the plot, it is very likely that these values are quite high for the respective schemer. This results in the following hypotheses:
9. Regarding the respective drama, the number of words, the number of speech acts, and the number of scenes of the schemer are the largest values.
10. Regarding the respective drama, the number of words, the number of speech acts, and the number of scenes of the schemer are among the three largest values.
2.3 Analysing Scheming Characters aside from the Scheming Male Slave
To better contextualise the trends for the scheming male slave, I also test the hypotheses for other intriguers. For this purpose, I have chosen every Roman comedy in which a scheming character appears, i.e., 23 out of 26 comedies. These comedies feature a wide range of schemers, such as plotting parasites, young men, old men, gods, hetaerae, a scheming married woman, or a plotting female slave. These characters serve as a point of comparison for the analysis of the scheming male slave.
2.4 Other Data Profiles
Fischer et al. analysed so-called “quantitative dominance relations” for 465 German dramas from 1730 until 1930 (Fischer et al. 2018, 193). For all characters of the respective play, they analysed the following network values: the degree centrality, weighted degree centrality, betweenness centrality, closeness centrality, and eigenvector centrality. The researchers also examined the following count-based measures: the number of scenes, number of speech acts, and the number of spoken words (Fischer et al. 2018, 194). They found that both types of measures ranked similarly high for protagonists (Fischer et al. 2018, 199). I will compare my findings with those of Fischer et al. as many scheming slaves in Roman comedy also act as protagonists.
3. Methodology
3.1 Text Selection
In the Roman comedies of Plautus and Terence from the 3rd and 2nd centuries BC, characters are frequently involved in intrigues, plots, and deceptions.13 In this article, the term “schemer” refers to characters who plot an intrigue. In Roman comedy, various word families refer to schemers and their plots, including the nouns dolus (“trick”) or consilium (“plan”) for a scheme, along with adjectives such as callidus or astutus to describe cunning, crafty, and clever schemers or plans. These word families tend to highlight a specific facet of scheming.14 However, there is no direct equivalent of the term “intrigue” in Roman comedy or other ancient literature, and no definition in the preserved ancient poetics (Dieterle 1980, 4).
While the aforementioned word families may indicate scheming in Roman comedy, it seems reasonable to further examine the concept of “intrigue” by exploring the structure of the intrigues in the surviving Roman comedies and their Greek models. Drawing on Arnulf Dieterle’s analysis of this structure, intrigue in Greco-Roman comedy can be defined as follows: An intrigue involves one character devising and carrying out a scheme against another character, using deception to achieve a particular goal (Dieterle 1980, 5). Additionally, Dieterle’s definition excludes any schemes that took place or started prior to the action of the play. He argues that the interaction between the schemer and their target must be part of the plot of the play, emphasising the significance of the target’s response to the intrigue (Dieterle 1980, 5). In the dramatic texts, however, characters use the same word families to refer to schemes occurring before and during the plot of the play. Therefore, the timing of the execution of an intrigue, whether before or during the action, does not determine the definition of an intrigue.15
When using the method of network analysis, I focus on the intrigues that occur throughout the play. This is because of how the network data is generated. The network data analysed is based on the co-occurrences of characters in a play as described by Pfister (Pfister 2001, 235–40). Moreover, it is static and thus represents the status at the end of the last scene. The automatised network analysis of the TEI-encoded text files of the Roman comedies comes with a limitation: It only detects those interactions between characters that can be identified by the speaker information in the text.16 Consequently, non-verbal interactions, as well as those reported but not shown on stage, are not considered, including pre-plot intrigues.17 Intrigues that unfold during a play, on the other hand, usually manifest themselves in the speeches of the characters involved. Therefore, network analysis appears to be a suitable method for studying schemers who carry out their plans during the course of a play, potentially providing new perspectives on these characters.
Turning to the scheming characters in Roman comedy, the slave plotting on behalf of a couple having an affair can be found in Plautus’ Asinaria, Bacchides, Epidicus, Miles gloriosus, Mostellaria, Persa, Poenulus, and Pseudolus, and Terence’s Adelphoe, Andria, and Heautontimoroumenos. Here the slave is plotting throughout the play, often dominating the comedy and greatly influencing the actions of other characters. Moreover, he usually enlists several helpers in his schemes. In Plautus’ Captivi, a supposed servus callidus schemes for his master for other reasons than an affair and eventually turns out to be freeborn. I will henceforth refer to such slaves as servi callidi in a narrower sense.
In addition to these striking schemers, some slaves demonstrate a momentary slyness or plot a brief intrigue without pursuing it any further. This is the case for Plautus’ Mercator and Trinummus. Also, a slave in Terence’s Phormio shows potential for scheming but is pushed aside by another intriguing character. We might understand these slave characters as servi callidi in a wider sense. Moreover, two slaves come into possession of money and intend to buy their freedom through a cleverly calculated plan. While they describe their actions as clever and smart (docte, astute, or similar), they cannot be labelled schemers in a narrower sense as they do not carry out a deceptive scheme like the other servi callidi but rather commit theft and lie about it.18 This applies to Plautus’ Aulularia and Rudens. In Plautus’ Amphitruo, the god Mercurius assumes the role of the servus callidus in the guise of a slave and plots throughout the play on the orders of his father Iuppiter. The latter initiated the superior doppelganger intrigue that he pursues throughout the play, thus also acting as a schemer.
Besides gods (dei), other characters also play the role of the intriguer, such as the eponymous parasites (parasiti) in Plautus’ Curculio and Terence’s Phormio, old men (senes) in Plautus’ Casina, Mercator, Trinummus, and Terence’s Andria, young men (adulescentes) in Plautus’ Menaechmi and Terence’s Eunuchus, a married woman (matrona) in Plautus’ Casina, hetaerae (meretrices) in Plautus’ Truculentus and Terence’s Eunuchus, and a female slave (ancilla) in Terence’s Eunuchus. The motives and aims of these schemers differ as do the extent and impact of their intrigues. I include the aforementioned plays in the selection as a point of comparison for the analysis of the cunning male slave. Plautus’ Cistellaria, Stichus, and Terence’s Hecyra19 do not feature any schemers acting on stage.
3.2 Source of the Text Files and Data
For my analysis, I used the Drama Corpora platform (DraCor), a digital infrastructure for programmable corpora (Börner and Trilcke 2023; Fischer et al. 2019). It contains several European drama corpora, including the Roman Drama Corpus (RomDraCor) (Beine and Fischer 2023). All texts are available as TEI-encoded text files. The texts of the comedies in the RomDraCor are based on already digitised and out-of-copyright editions, Leo’s edition of Plautine plays (Plautus 1895–1896) and Parry’s edition of Terentian comedies (Terence 1857). Although these editions date from the 19th century, the texts are qualified for digital analysis and distant reading.
Most importantly, DraCor provides an Application Programming Interface (API) through which users can extract specific parts of or information about dramatic texts within the DraCor infrastructure, such as network data or count-based data. The DraCor API thus proves suitable for the digital analysis of the selected Roman comedies.
For instance, the DraCor API computes network data for a play using the Python package NetworkX (Hagberg et al. 2008; Börner and Trilcke 2023, 52–54). The network data itself is derived from the co-occurrences of speaking characters in a play as described in the previous section. The calculation of the network data only takes into account the co-occurrence of speaking characters in a scene, not the number of words spoken between them. Furthermore, the network data is static, thus reflecting the status at the end of the final scene.
3.3 Processing the Network Data and Count-Based Data
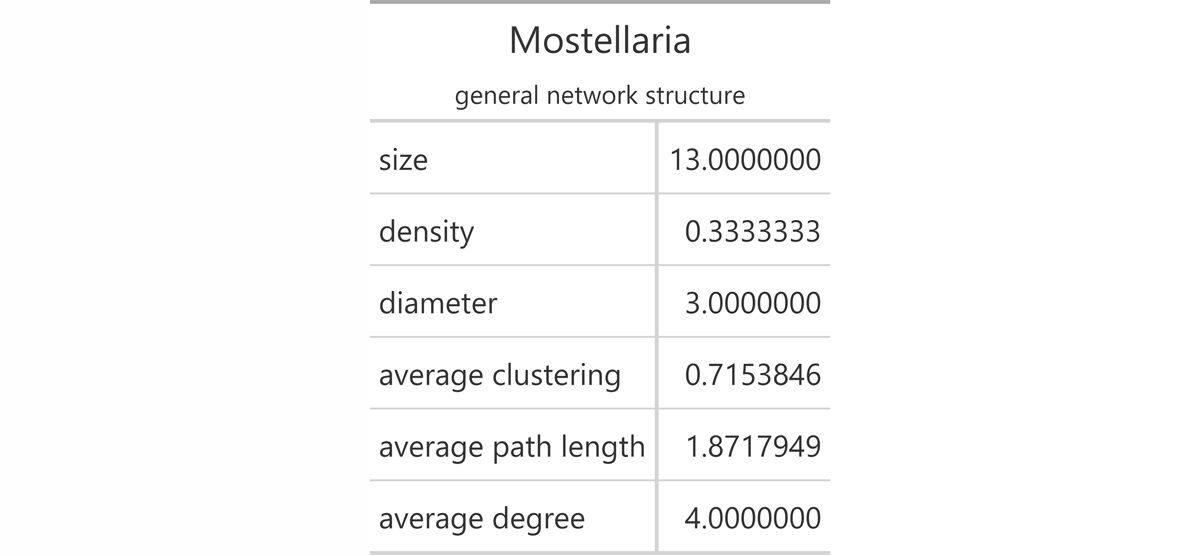
For my analysis in R (R Core Team 2023), I mainly worked with the packages rdracor (Pozdniakov and Fischer 2023), tidyverse (Wickham et al. 2019), gt (Iannone et al. 2023), igraph (Csárdi et al. 2023), ggraph (Pedersen 2022), and RColorBrewer (Neuwirth 2022). First, I used the rdracor package to get the data from the DraCor API (DraCor 2023). Via the function “get_play_metadata”, I retrieved the general network values for the respective network, namely the size, density, diameter, average clustering coefficient, average path length, and average degree. With the gt package, I then created a table entitled “general network structure” for each play in my corpus. For illustration, see Figure 1.
Via the rdracor function “get_net_cooccur_igraph”, I retrieved an igraph object based on a co-occurrence matrix as described above. It already included some of the data of interest for my analysis, such as the degree centrality, weighted degree centrality, closeness centrality, and betweenness centrality as well as the number of words, number of speech acts, and number of scenes per character. To these node attributes or vertex attributes, I added the clustering coefficient for each character which I calculated via the “transitivity” function of igraph. I also calculated the number of triangles for each character via the igraph function “count_triangles” and added it as a node attribute.
Furthermore, I added the character type as a node attribute manually. The type categories are based on the lists of dramatis personae in Leo’s and Parry’s editions (Plautus 1895–1896; Terence 1857). I have modified a few for consistency, e.g., I changed uxor to matrona.
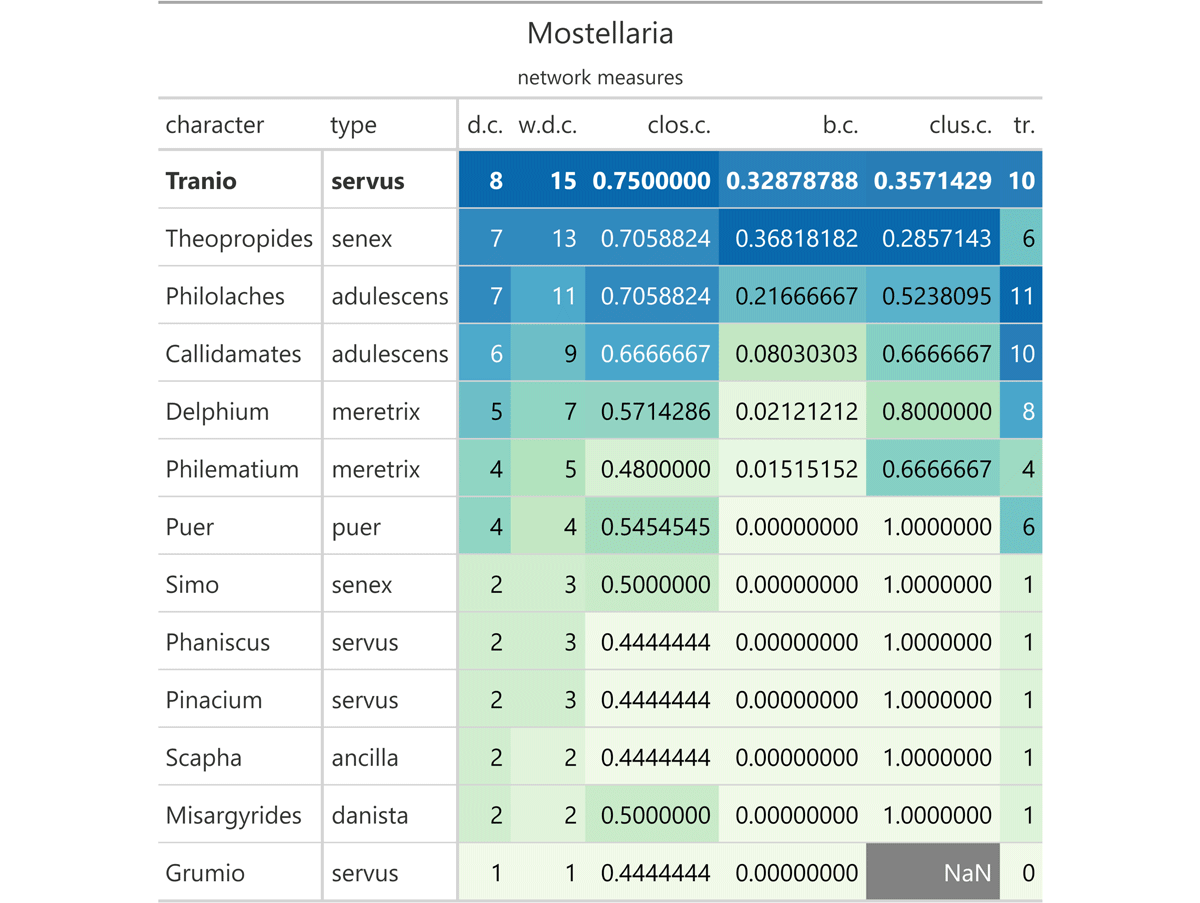
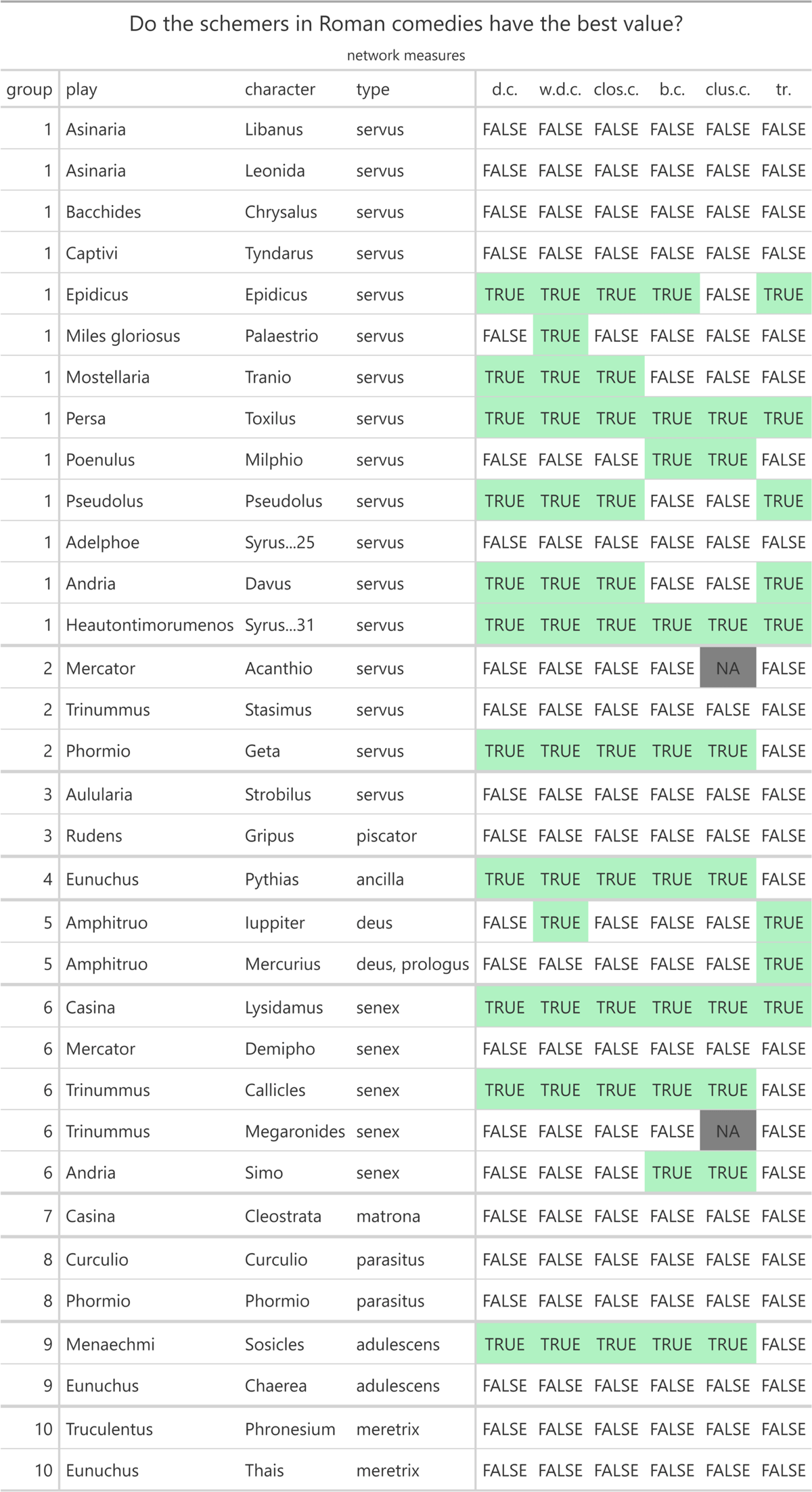
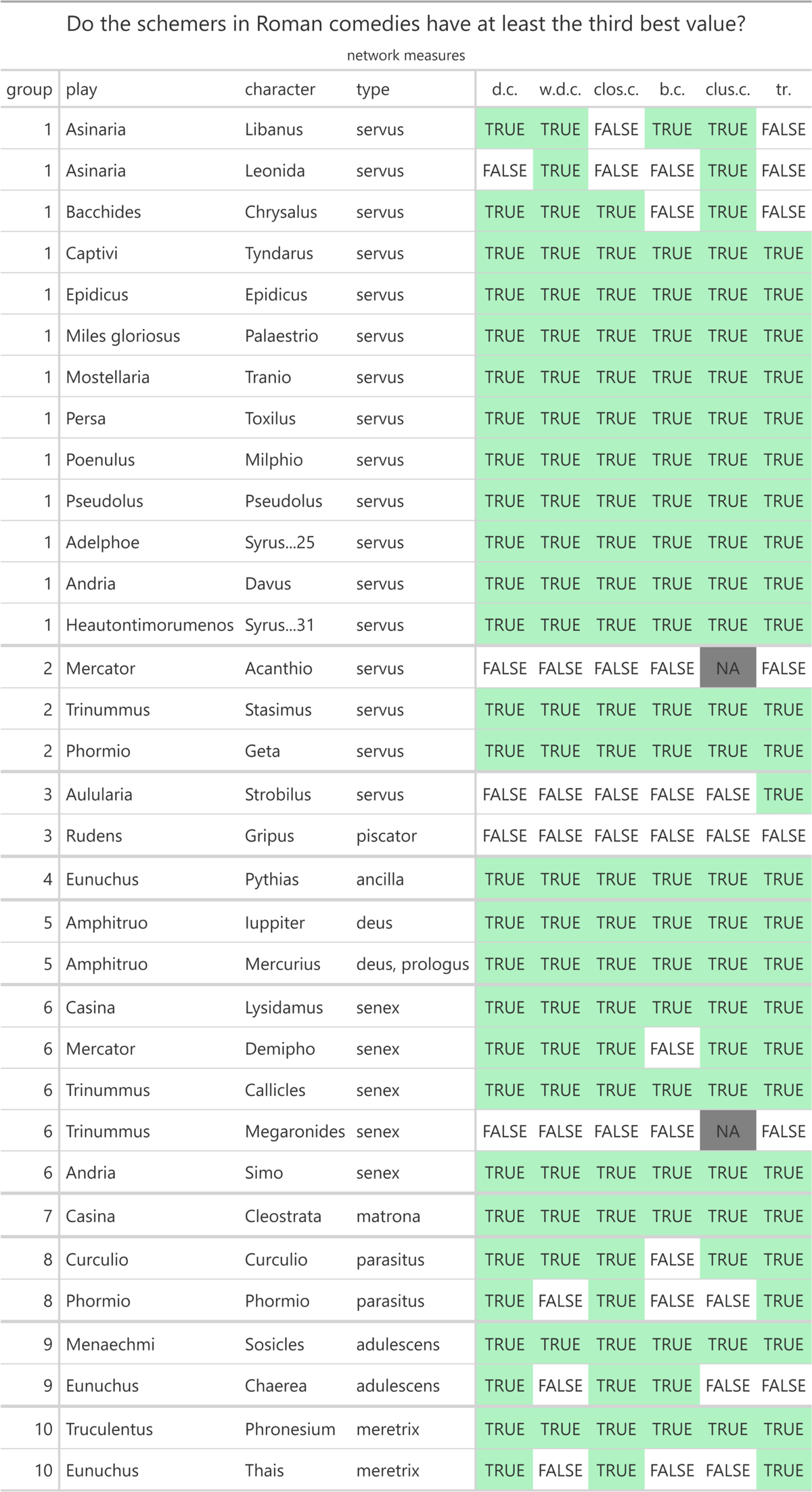
From this data, I created two more tables with the gt package for each play. One is entitled “network measures” and shows the network values of each character in the respective play, namely the degree centrality, weighted degree centrality, closeness centrality, betweenness centrality, clustering coefficient, and number of triangles. This table is sorted in descending order according to the degree centrality and the weighted degree centrality. Moreover, I coloured the cells of the table using a Brewer colour palette via the RColorBrewer package. The higher the degree centrality, weighted degree centrality, closeness centrality, betweenness centrality, and the number of triangles, the darker the colour of the cell; the lower the clustering coefficient, the darker the cell. Finally, I highlighted the row(s) with the values of the schemer(s) in bold. For illustration, see the table for Plautus’ Mostellaria which features the scheming slave Tranio (Figure 2).
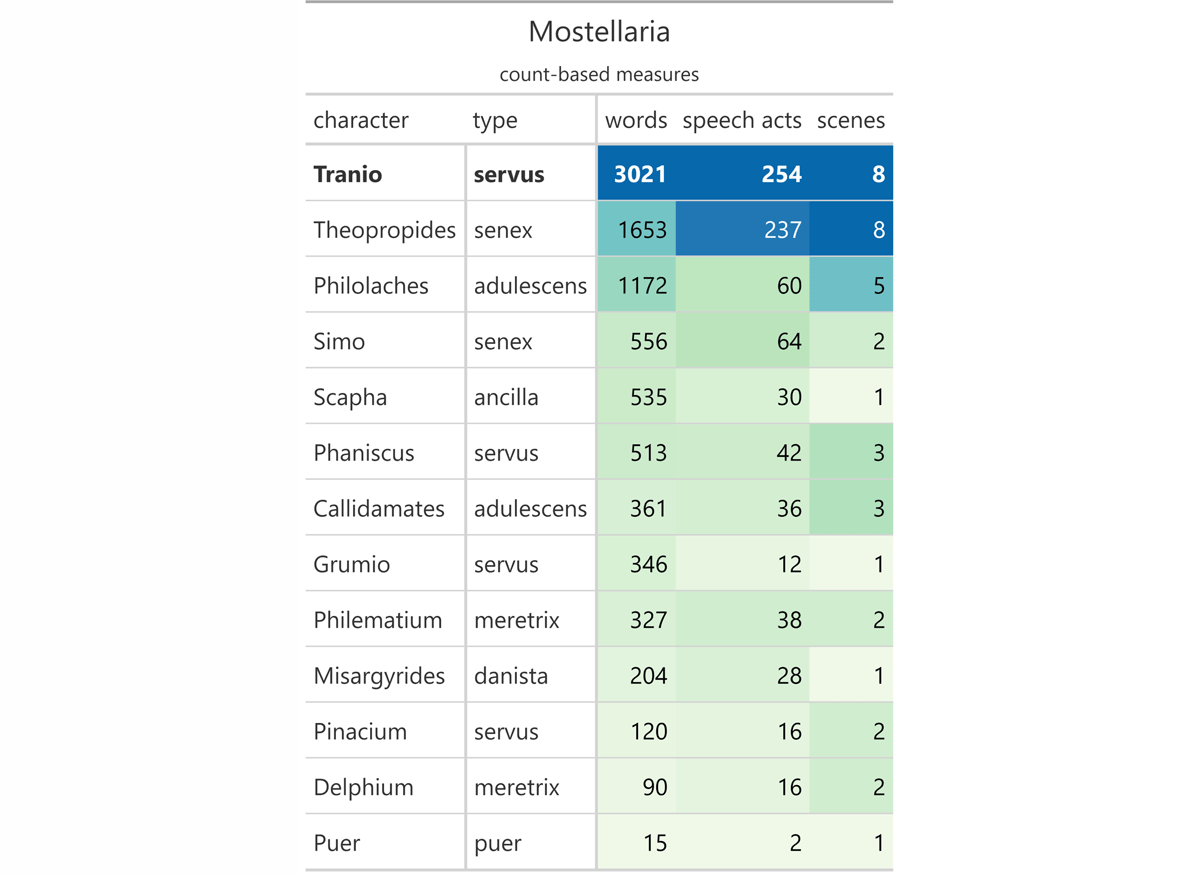
The other table displays the count-based values per character, the number of words, the number of speech acts, and the number of scenes per character and is entitled “count-based measures”. It is arranged in descending order by the number of words spoken and the number of speech acts. Here I used the Brewer colour palette as well. The higher the number, the darker the cell. Eventually, I highlighted the row(s) with the values of the schemer(s) in bold. For illustration, see Figure 3.
I then prepared the overall evaluation of the data.20 According to the hypotheses, the degree centrality, weighted degree centrality, closeness centrality, betweenness centrality, and the number of triangles of a schemer should be at least the third highest value respectively while the clustering coefficient should be at least the third lowest value. This is why I first inversed the values of the clustering coefficient before using the function “dense_rank” to rank the characters of a play. Following the hypotheses, the most advantageous value for a schemer should get the rank “1” respectively, so I inversed the ranks. Depending on the hypothesis, I then checked whether characters rank first or at least third best respectively which returned a data frame with the entries “TRUE” or “FALSE” for all characters of a play. From this data frame, I extracted the row(s) with the values of the schemer(s). For the overall evaluation, I combined the rows with the values of the schemers from the individual plays into one table for all selected Roman comedies. I also added a column with the character group of each character as explained below. This column made it possible to sort the schemers according to their character group for a better overview. I used the same method to evaluate the count-based data.
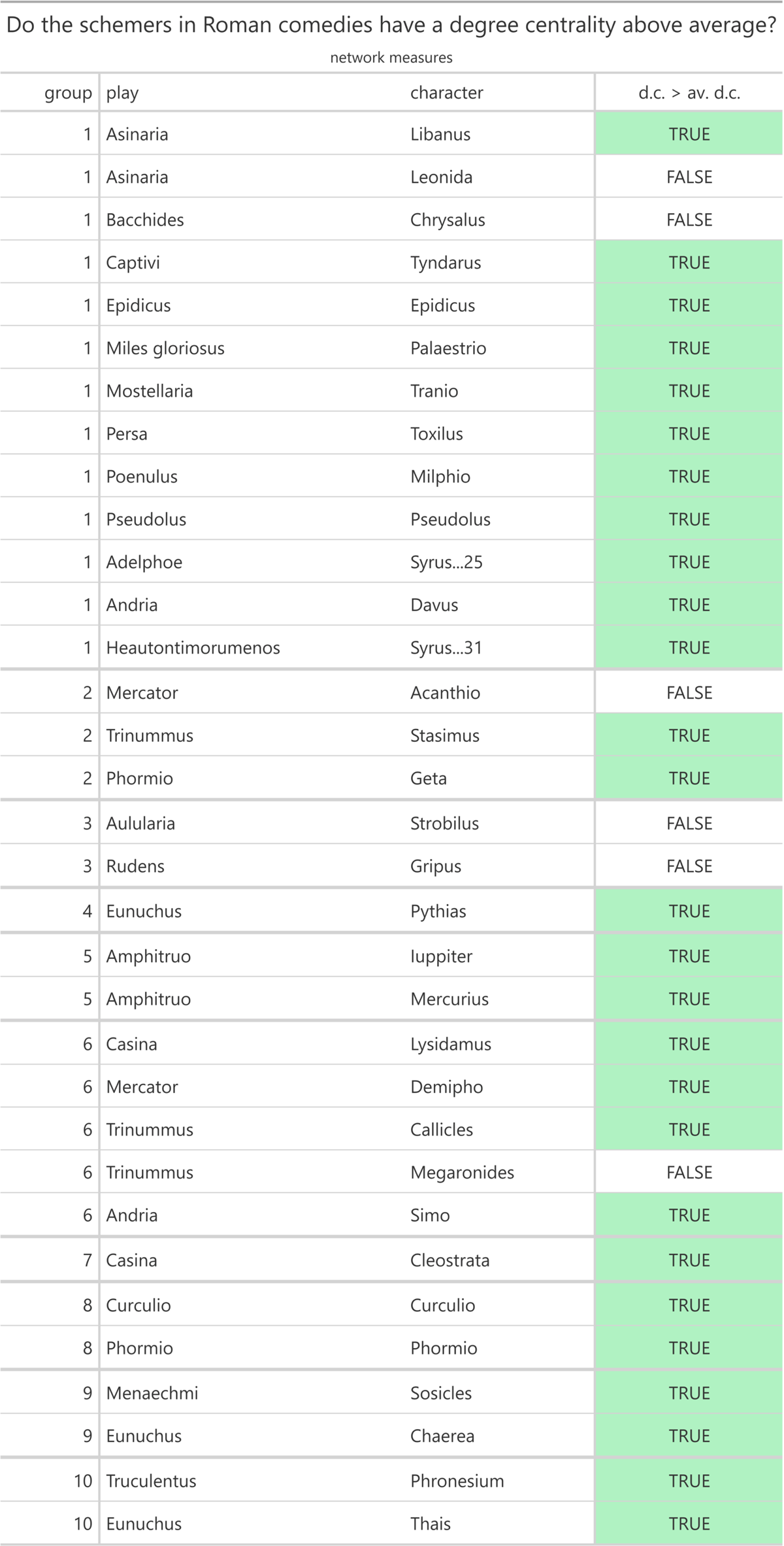
I also checked whether the degree centrality is above average for all characters of a play via the dplyr function “transmute”. I then extracted the row(s) with the values of the schemer(s). Similar to the procedure described above, I then combined the rows with the values of the schemers from the individual plays into one table for all selected Roman comedies. I used the same method to check whether the clustering coefficient is below average for the schemers. This way, I created six tables for the evaluation of the selected Roman comedies. In all evaluation tables, cells with “TRUE” are highlighted in green.
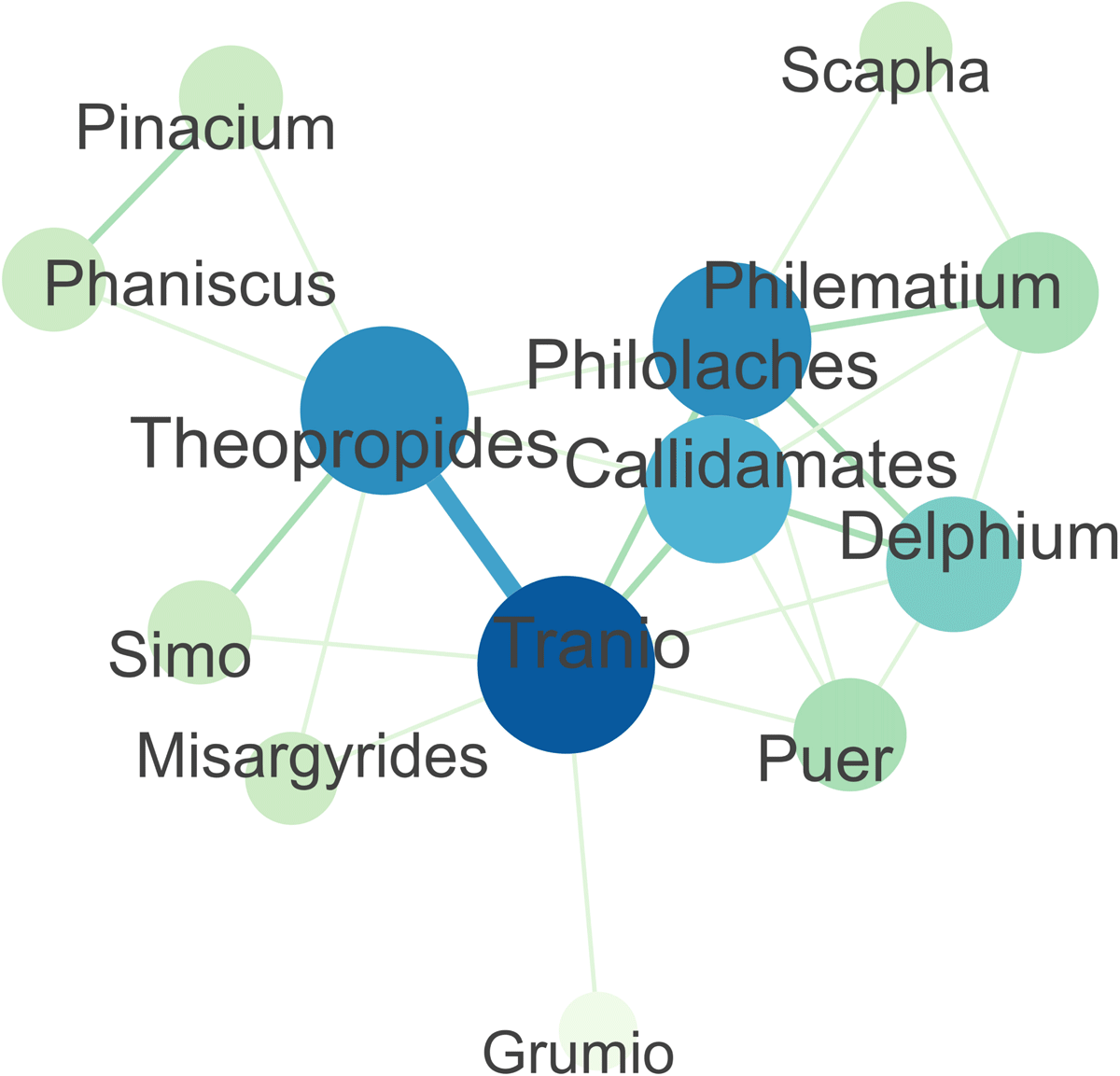
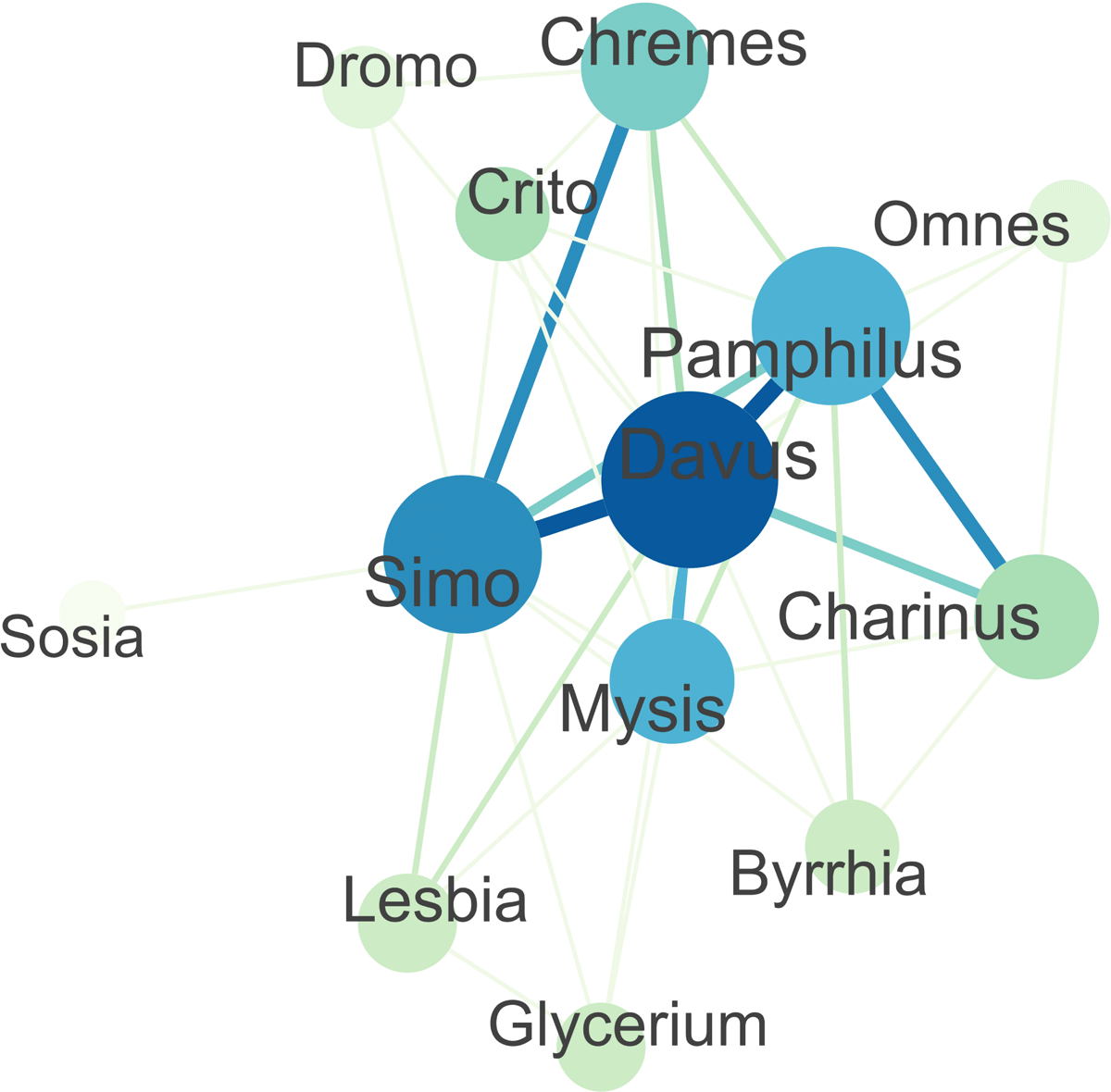
To create the network graph, I used the package ggraph. Here I chose the layout algorithm “stress”. I then specified the layout of the nodes and edges as follows. The more often two characters interact with each other, the thicker the edge between the corresponding nodes. The weight of the edge also determines its colour. Drawing on the Brewer colour palette, an edge is coloured darker the greater its weight. Regarding the layout of the nodes, the colour of a node corresponds to its degree centrality: The higher the latter, the darker the former. The size of a node depends on its weighted degree centrality. The more weight the edges or relations of a character have, the larger the corresponding node is. For illustration, see the network graph for Plautus’ Mostellaria with the scheming slave Tranio (Figure 4).
Some of the analysed Roman comedies have a particular feature which illustrates how the conventions of Roman comedy influence the network data. Here the context of the performance becomes part of the comedy occasionally. For instance, members of the production team are included in the text, such as the choragus in Plautus’ Curculio. Sometimes, the troupe of actors (caterva, grex, or omnes) or possibly the playwright (poeta) addresses the audience at the end of the last scene of a play to ask for applause and thus closes the play. This is the case for Plautus’ comedies Asinaria, Bacchides, Captivi, Cistellaria, Epidicus, Trinummus, and all of Terence’s comedies. Therefore, the actors fall out of their roles within the last scene. This results in a particular feature of the respective network graphs. The node of the caterva, grex, omnes, or poeta is connected to the characters of the last scene, so the actors are connected to the characters as which they performed right before their farewell to the audience. For illustration, see the network graph for Terence’s Andria which features the scheming slave Davus and shows a node named “Omnes” (Figure 5).
The three tables with the general network values, the character-specific network values, and the character-specific count-based values, together with the network graph, form a dataset for each play. All datasets can be accessed online (see section 7).
4. Results
Regarding the Roman comedies, I checked the hypotheses for the following character groups:
scheming male slaves (servi callidi) in a narrower sense: Libanus (Asinaria), Leonida (Asinaria), Chrysalus (Bacchides), Tyndarus (Captivi), Epidicus (Epidicus), Palaestrio (Miles gloriosus), Tranio (Mostellaria), Toxilus (Persa), Milphio (Poenulus), Pseudolus (Pseudolus), Syrus (Adelphoe), Davus (Andria), and Syrus (Heautontimoroumenos);
scheming male slaves (servi callidi) in a wider sense: Acanthio (Mercator), Stasimus (Trinummus), and Geta (Phormio);
clever male slaves (servi callidi) who want to buy their freedom with someone else’s money: Strobilus (Aulularia)21 and Gripus (Rudens);
scheming female slaves (ancillae callidae): Pythias (Eunuchus);
scheming gods (dei callidi): Iuppiter and Mercurius (both Amphitruo);
scheming old men (senes callidi): Lysidamus (Casina), Demipho (Mercator), Callicles (Trinummus), Megaronides (Trinummus), and Simo (Andria);
scheming married women (matronae callidae): Cleostrata (Casina);
scheming parasites (parasiti callidi): Curculio (Curculio), Phormio (Phormio);
scheming young men (adulescentes callidi): Sosicles (Menaechmi) and Chaerea (Eunuchus);
scheming hetaerae (meretrices callidae): Phronesium (Truculentus) and Thais (Eunuchus).
1st hypothesis
To check the first hypothesis, we analyse the table entitled “Do the schemers in Roman comedies have the best value?” and subtitled “network measures”, more precisely the columns “d.c.”, “w.d.c.”, “clos.c.”, and “b.c.” (Figure 6). We will focus first on the cunning male slaves (servi callidi), namely the scheming male slaves in a narrower sense, the scheming male slaves in a wider sense, and the clever male slaves who want to buy their freedom with someone else’s money. Secondly, we will look at the other scheming characters.
In the group of the scheming male slaves (servi callidi) in a narrower sense, 3 out of 13 characters (ca. 23%) have the highest degree centrality, weighted degree centrality, closeness centrality, and betweenness centrality respectively, thus confirming all the assumptions of the first hypothesis. Regarding the scheming male slaves (servi callidi) in a wider sense, the first hypothesis applies to one of three characters. On the other hand, the first hypothesis is not true for the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money.
Looking at the other scheming characters, the first hypothesis applies to the only scheming female slave (ancilla callida). Among the five scheming old men (senes callidi), two characters meet the first hypothesis. Concerning the scheming young men (adulescentes callidi), the first hypothesis is true for one of the two characters. By contrast, the first hypothesis is not true for the only scheming married woman (matrona callida), the two scheming gods (dei callidi), the two scheming parasites (parasiti callidi), and the two scheming hetaerae (meretrices callidae).
2nd hypothesis
To test the second hypothesis, we evaluate the table entitled “Do the schemers in Roman comedies have at least the third best value?” and subtitled “network measures”, more specifically the columns “d.c.”, “w.d.c.”, “clos.c.”, and “b.c.” (Figure 7).
Regarding the scheming male slaves (servi callidi) in a narrower sense, 10 out of 13 characters (ca. 77%) fulfill all aspects of the second hypothesis by having at least the third highest degree centrality, weighted degree centrality, closeness centrality, and betweenness centrality respectively. Looking at the measures individually, it seems remarkable that all 13 characters (100%) have at least the third highest weighted degree centrality, 12 of the 13 characters (ca. 92%) have at least the third highest degree centrality, and 11 of the 13 characters (ca. 85%) have at least the third highest closeness centrality which also applies to the betweenness centrality. In the group of the scheming male slaves (servi callidi) in a wider sense, the hypothesis can be confirmed for two of the three characters. However, the second hypothesis is not true for the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money.
Considering the other scheming characters apart from the male slaves, the second hypothesis applies to the only scheming female slave (ancilla callida), the only scheming married woman (matrona callida), and both scheming gods (dei callidi). Other character types partly meet the second hypothesis, three out of five scheming old men (senes callidi), one out of two scheming young men (adulescentes callidi), and one out of two scheming hetaerae (meretrices callidae). Neither of the scheming parasites (parasiti callidi) fulfills all the assumptions of the second hypothesis.
3rd hypothesis
To check the third hypothesis, we look at the table entitled “Do the schemers in Roman comedies have a degree centrality above average?” (Figure 8). As before, we start with the cunning male slaves.
11 out of 13 scheming male slaves (servi callidi) in a narrower sense (ca. 85%) meet the third hypothesis. Regarding the scheming male slaves (servi callidi) in a wider sense, the third hypothesis is true for two out of three characters. By contrast, neither of the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money fulfills the third hypothesis.
Among the other scheming characters, the third hypothesis is true for the only scheming female slave (ancilla callida), the only scheming married woman (matrona callida), both scheming gods (dei callidi), both scheming parasites (parasiti callidi), both scheming young men (adulescentes callidi), and both scheming hetaerae (meretrices callidae). Moreover, four of the five scheming old men (senes callidi) meet the third hypothesis.
4th hypothesis
To test the fourth hypothesis, we interpret the table entitled “Do the schemers in Roman comedies have the best value?”, more specifically the columns “clus.c.” and “tr.” (Figure 6).
Regarding the scheming male slaves (servi callidi) in a narrower sense, 2 out of 13 characters (ca. 15%) have the lowest clustering coefficient and the largest number of triangles, thus fulfilling the fourth hypothesis. On the other hand, the fourth hypothesis is neither true for the scheming male slaves (servi callidi) in a wider sense nor for the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money.
Looking at the other scheming characters besides the male slaves, just one scheming old man (senex callidus) fulfills the two assumptions of the fourth hypothesis, while it cannot be confirmed for the four other scheming old men (senes callidi), nor for the only scheming female slave (ancilla callida), nor the only scheming married woman (matrona callida), for neither of the scheming gods (dei callidi), neither of the scheming parasites (parasiti callidi), neither of the scheming young men (adulescentes callidi), and neither of the scheming hetaerae (meretrices callidae).
5th hypothesis
To check the fifth hypothesis, we analyse the table entitled “Do the schemers in Roman comedies have at least the third best value?” and subtitled “network measures”, more precisely the columns “clus.c.” and “tr.” (Figure 7). The cunning male slaves will be considered first.
In the group of the scheming male slaves (servi callidi) in a narrower sense, 10 out of 13 characters (ca. 77%) meet the fifth hypothesis by having at least the third lowest clustering coefficient and at least the third largest number of triangles. Remarkably, even all 13 characters (100%) have at least the third lowest clustering coefficient. Concerning the scheming male slaves (servi callidi) in a wider sense, the fifth hypothesis is true for two of the three characters. However, neither of the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money confirms the fifth hypothesis.
Among the other scheming characters, the fifth hypothesis is true for the only scheming female slave (ancilla callida), the only scheming married woman (matrona callida), and both scheming gods (dei callidi). The remaining character types partly fit the fifth hypothesis, four of five scheming old men (senes callidi), one of two scheming parasites (parasiti callidi), one of two scheming young men (adulescentes callidi), and one of two scheming hetaerae (meretrices callidae).
6th hypothesis
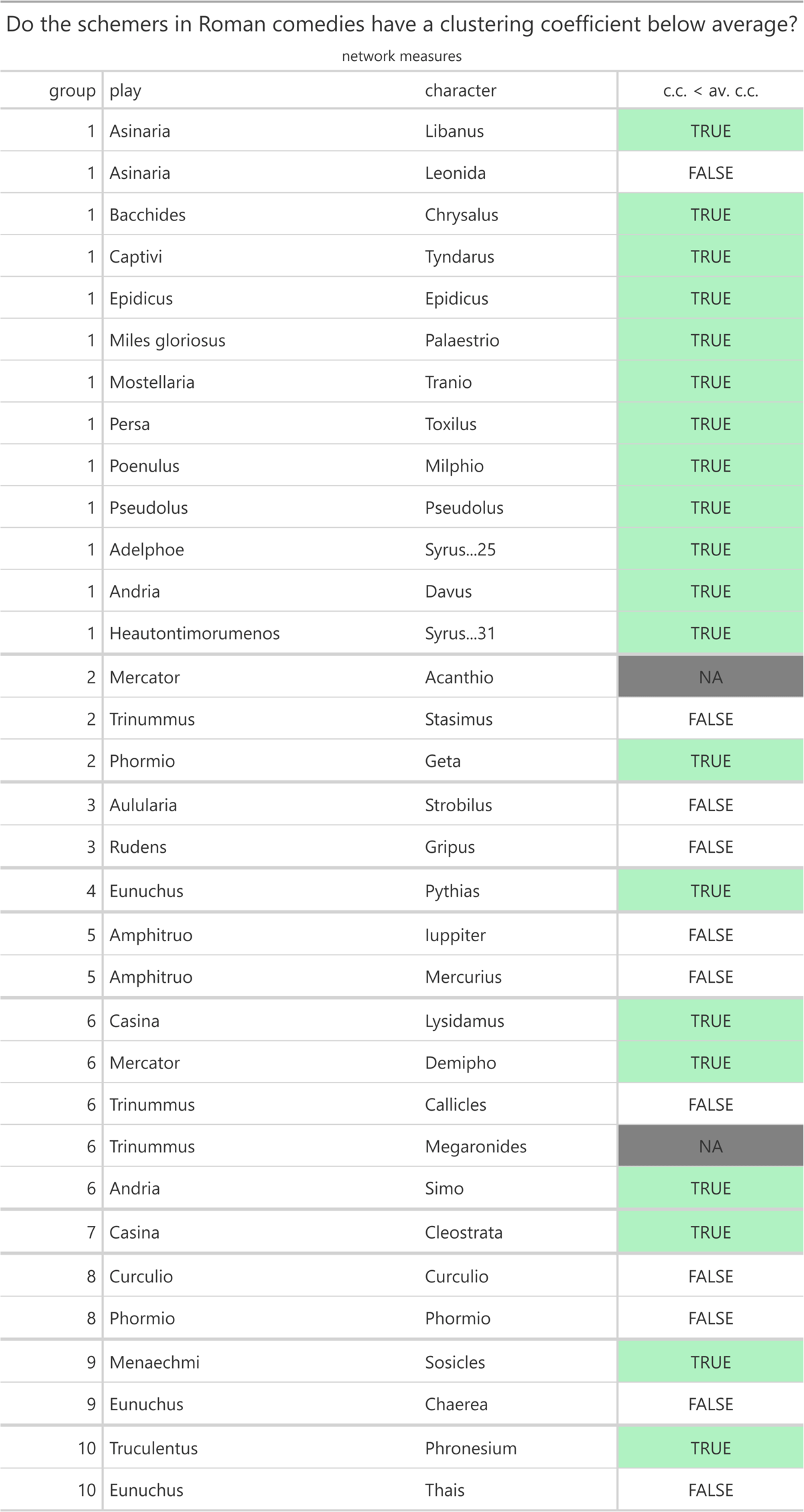
To test the sixth hypothesis, we look at the table entitled “Do the schemers in Roman comedies have a clustering coefficient below average?” (Figure 9). As usual, we begin with the cunning male slaves.
Regarding the scheming male slaves (servi callidi) in a narrower sense, the sixth hypothesis is true for 12 out of 13 characters (ca. 92%). Moreover, one out of three scheming male slaves (servi callidi) in a wider sense meets the sixth hypothesis. By contrast, the sixth hypothesis is not true for the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money.
Among the other scheming characters, the sixth hypothesis applies to the only scheming female slave (ancilla callida) and the only scheming married woman (matrona callida). Certain character types partly fulfill the sixth hypothesis, with three out of five scheming old men (senes callidi), one out of two scheming young men (adulescentes callidi), and one out of two scheming hetaerae (meretrices callidae) having a clustering coefficient below average. On the other hand, neither of the scheming gods (dei callidi) and neither of the scheming parasites (parasiti callidi) fit the sixth hypothesis.
7th hypothesis
To check the seventh hypothesis, we evaluate the table entitled “Do the schemers in Roman comedies have the best value?” and subtitled “network measures”, more precisely the columns “b.c.” and “clus.c.” (Figure 6). As before, we start with the cunning male slaves.
Looking at the scheming male slaves (servi callidi) in a narrower sense, 3 out of 13 characters (ca. 23%) have the highest betweenness centrality and the lowest clustering coefficient, thus fulfilling the seventh hypothesis. Regarding the scheming male slaves (servi callidi) in a wider sense, the seventh hypothesis applies to one out of three characters. However, the seventh hypothesis is not true for the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money.
Looking at the other scheming characters, the only scheming female slave (ancilla callida) meets the seventh hypothesis. Furthermore, the seventh hypothesis applies to three out of five scheming old men (senes callidi) and to one out of two scheming young men (adulescentes callidi). By contrast, the seventh hypothesis is not true for the only scheming married woman (matrona callida), the scheming gods (dei callidi), the scheming parasites (parasiti callidi), nor for the scheming hetaerae (meretrices callidae).
8th hypothesis
To test the eighth hypothesis, we analyse the table entitled “Do the schemers in Roman comedies have at least the third best value?” and subtitled “network measures”, more specifically the columns “b.c.” and “clus.c.” (Figure 7). First, we concentrate on the cunning male slaves.
Among the scheming male slaves (servi callidi) in a narrower sense, 11 out of 13 characters (ca. 85%) meet the eighth hypothesis by having at least the third highest betweenness centrality and at least the third lowest clustering coefficient. Note that even all of these slaves (100%) have at least the third lowest clustering coefficient. Regarding the scheming male slaves (servi callidi) in a wider sense, the eighth hypothesis is true for two out of three characters. On the other hand, the eighth hypothesis is not true for the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money.
Turning to the other scheming characters, the eighth hypothesis applies to the only scheming female slave (ancilla callida), the only scheming married woman (matrona callida), and both scheming gods (dei callidi). Other character types partly meet the eighth hypothesis, three out of five scheming old men (senes callidi), one out of two scheming young men (adulescentes callidi), and one out of two scheming hetaerae (meretrices callidae). However, the eighth hypothesis is not true for the scheming parasites (parasiti callidi).
9th hypothesis
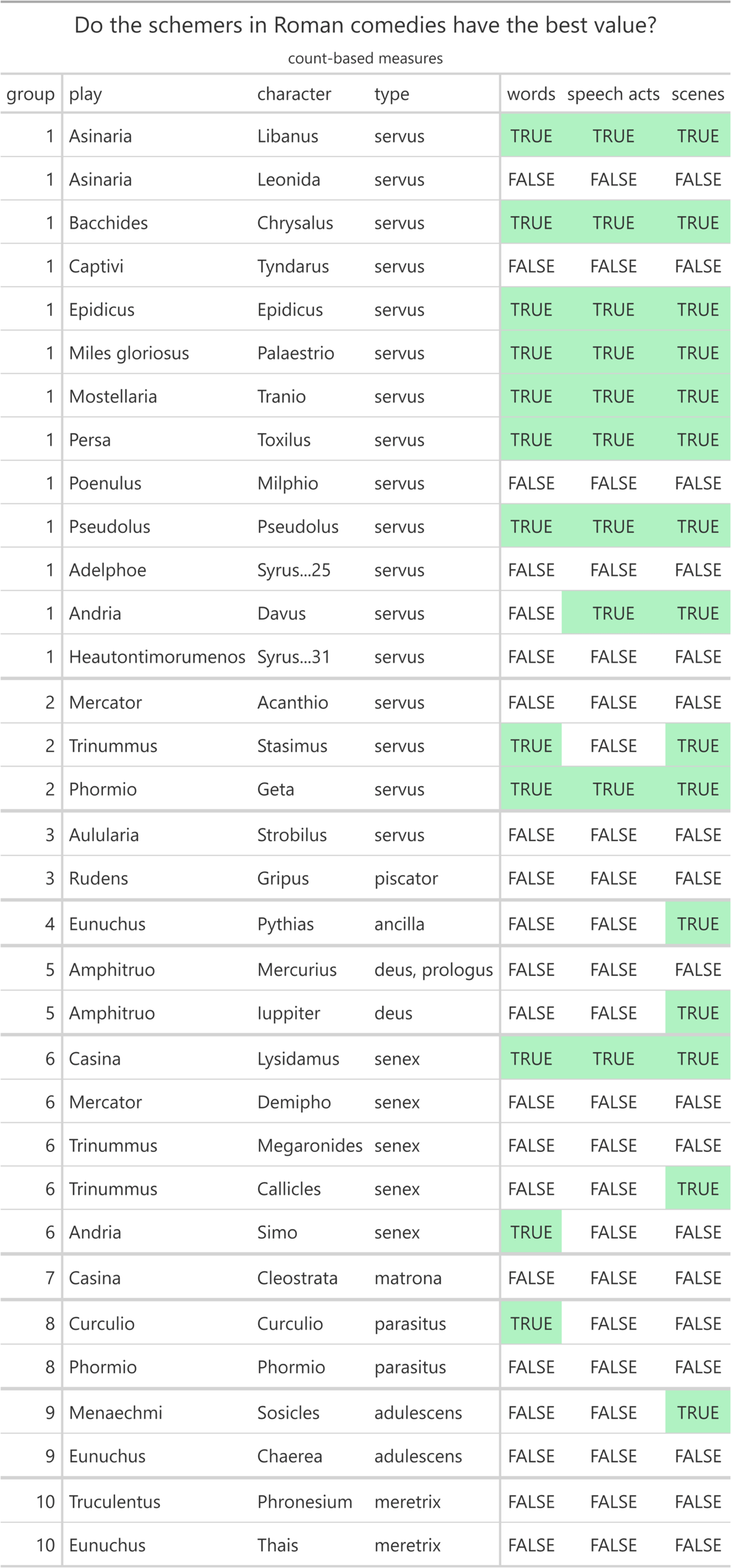
To check the ninth hypothesis, we interpret the table which is entitled “Do the schemers in Roman comedies have the best value?” and subtitled “count-based measures” (Figure 10). We turn to the cunning male slaves first.
Regarding the scheming male slaves (servi callidi) in a narrower sense, 7 out of 13 characters (ca. 54%) have the largest number of spoken words, the largest number of speech acts, and the largest number of scenes in which they appear, thus fitting the ninth hypothesis. In the group of the scheming male slaves (servi callidi) in a wider sense, one out of three characters confirms all assumptions of the ninth hypothesis. On the other hand, the ninth hypothesis is not true for either of the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money.
Among the other scheming characters, just one scheming old man (senex callidus) fits all aspects of the ninth hypothesis, whereas the hypothesis cannot be confirmed for the other four scheming old men (senes callidi), nor for the only scheming female slave (ancilla callida), nor the only scheming married woman (matrona callida), for neither of the scheming gods (dei callidi), neither of the scheming parasites (parasiti callidi), neither of the scheming young men (adulescentes callidi), and neither of the scheming hetaerae (meretrices callidae).
10th hypothesis
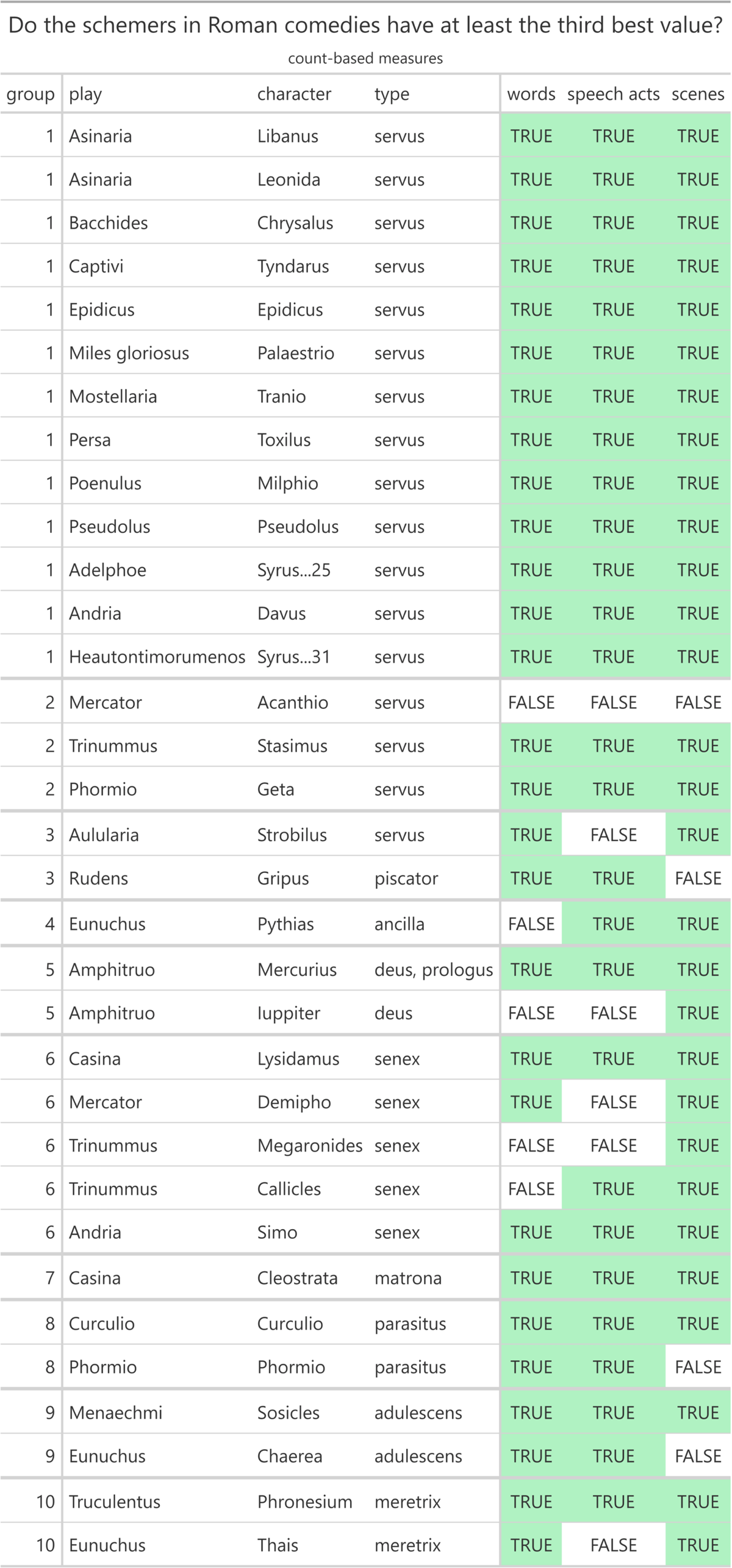
To test the tenth hypothesis, we analyse the table which is entitled “Do the schemers in Roman comedies have at least the third best value?” and subtitled “count-based measures” (Figure 11).
Looking at the scheming male slaves (servi callidi) in a narrower sense, all 13 characters (100%) have at least the third largest number of spoken words, at least the third largest number of speech acts, and at least the third largest number of scenes in which they appear, thus confirming all assumptions of the tenth hypothesis. Moreover, the tenth hypothesis is true for two of the three scheming male slaves (servi callidi) in a wider sense. On the other hand, the clever male slaves (servi callidi) who want to buy their freedom with someone else’s money do not fit all aspects of the tenth hypothesis.
Considering the other scheming characters, the tenth hypothesis applies to the only scheming married woman (matrona callida). Some of the other character types also fit all aspects of the tenth hypothesis, namely two of the five scheming old men (senes callidi), one of the two scheming gods (dei callidi), one of the two scheming parasites (parasiti callidi), one of the two scheming young men (adulescentes callidi), and one of the two scheming hetaerae (meretrices callidae). The only scheming female slave (ancilla callida) does not confirm all assumptions of the tenth hypothesis.
5. Discussion
5.1 Data Trends for Scheming Slaves in Roman Comedy
Regarding Roman comedy, we can work out general data trends for the scheming male slaves (servi callidi) in a narrower sense. Three out of 13 characters show the strongest centralisation with having the highest degree centrality, weighted degree centrality, closeness centrality, and betweenness centrality. Looking at the centrality measures individually, between four and seven scheming male slaves (servi callidi) have the highest value respectively (1st hypothesis). What is more, 10 out of 13 characters have at least the third highest degree centrality, weighted degree centrality, closeness centrality, and betweenness centrality (2nd hypothesis). From this, we can deduce that there is a high centralisation on the scheming male slaves (servi callidi) in the respective dramatic network. Therefore, the scheming male slaves (servi callidi) can perform a coordinating role. Moreover, 11 out of 13 characters have a degree centrality above average and thus interact verbally with more different characters than average (3rd hypothesis).
The scheming male slaves (servi callidi) in a narrower sense also have a potentially advantageous position in the respective dramatic network. Three out of 13 characters have the highest betweenness centrality and the lowest clustering coefficient while even 11 out of 13 characters have at least the third highest betweenness centrality and at least the third lowest clustering coefficient. They can therefore act as brokers and manipulators (7th and 8th hypothesis).
In particular, they can exert power over other characters by playing one against another. This is shown by all 13 characters having at least the third lowest clustering coefficient with three of the 13 having the lowest (4th and 5th hypothesis). Furthermore, 12 of the 13 characters have a clustering coefficient below average (6th hypothesis). At the same time, 10 of the 13 characters have at least the third largest number of triangles with five of them even having the largest (4th and 5th hypothesis). In this group of scheming male slaves, Leonida (Asinaria) falls out of almost all data trends. The reason for this might be that although Leonida pursues a plan of intrigue, he is not the main schemer, but his fellow slave Libanus is.
In terms of count-based measures, the scheming male slaves (servi callidi) in a narrower sense are very present throughout the play and tend to dominate the stage. This is demonstrated by the fact that all 13 characters have at least the third largest number of spoken words, speech acts, and scenes with seven of them even having the highest values respectively (9th and 10th hypothesis).
Regarding the scheming male slaves (servi callidi) in a wider sense, we find the trends mentioned above partly for two of three characters. Stasimus (Trinummus) and Geta (Phormio) show the trend of centralisation (1st and 2nd hypothesis) and interact with more different characters than average (3rd hypothesis). The same two characters have at least the third highest betweenness centrality and at least the third lowest clustering coefficient and thus can act as brokers and as manipulators (7th and 8th hypothesis). Looking at the count-based measures, their values are at least the third largest. Thus, we also find a trend of large presence and dominance throughout the play (9th and 10th hypothesis). However, we find none of the trends for Acanthio (Mercator). The reason for this is that this slave only appears in one scene at the beginning of the play to tell his young master about the intrigue he has started. The young man then continues the intrigue with the help of a friend.
For the clever male slaves (servi callidi) who plan to buy their freedom with someone else’s money, we cannot confirm the data profile concerning the network measures. Looking at the count-based measures, we only get mixed results. Hence, the data profile does not apply to this type of character. This observation is not surprising as these characters do not intrigue in the usual sense.
By contrast, we find largely the same data trends for the scheming female slave (ancilla callida) as for the scheming male slaves (servi callidi). The only exception is the number of spoken words which is not at least one of the three largest values (10th hypothesis).
Based on these observations, we can confirm the following data profile for the scheming male and female slaves:
In the respective network, there is a strong centralisation on the scheming slave since the schemer tends to have at least the third highest centralities (2nd hypothesis).
The scheming slave also interacts with many different characters as he/she tends to have a degree centrality above average and at least the third largest number of triangles (3rd hypothesis and part of the 5th hypothesis).
The scheming slave can easily play other characters against each other since he/she tends to have a clustering coefficient below average and at least the third lowest clustering coefficient (6th hypothesis and part of the 5th and 8th hypothesis).
The scheming slave can have the potentially advantageous position of a broker and a manipulator as he/she tends to have at least the third highest betweenness centrality and at least the third lowest clustering coefficient (8th hypothesis).
The scheming slave dominates the stage since he/she tends to have at least the third largest number of spoken words, speech acts, and scenes (10th hypothesis).
This data profile seems remarkable given the status of the scheming slave in the group of the dramatis personae. In classical antiquity, a slave was considered property and had to obey his/her owner, something that is echoed in Roman comedy. Here, however, the scheming slave acquires a considerable amount of social capital in the course of the action, as shown by the network values that depict the status at the end of the play. This social capital gives him/her the possibility to exert power over other characters and to direct the plot in his/her favour—an opportunity that the scheming slave is all too ready to seize.22
5.2 Data Trends for Other Scheming Characters in Roman Comedy
For comparison, we also evaluated the data for scheming characters other than slaves. For the scheming gods (dei callidi), the data profile can be largely confirmed for Mercurius (2nd, 3rd, 5th, 8th, and 10th hypothesis), except for a clustering coefficient below average (6th hypothesis). This is consistent with the fact that Mercurius explicitly adopts the role of the scheming slave (servus callidus) as a doppelganger. Concerning the network measures, Iuppiter also shows most of the data trends in question (2nd, 3rd, 5th, and 8th hypothesis). For the scheming married woman (matrona callida), Cleostrata (Casina), all of the data trends can be found (2nd, 3rd, 5th, 6th, 8th, and 10th hypothesis). This puts her on par with her scheming husband Lysidamus (Casina).
For the other character types, we generally get a mixed impression. Concerning the scheming old men (senes callidi), two of five characters show all the data trends in question, Simo (Andria) and Lysidamus (Casina) (2nd, 3rd, 5th, 6th, 8th, and 10th hypothesis). Regarding the scheming young men (adulescentes callidi), we find all the data trends for Sosicles (Menaechmi), but not for Chaerea (Eunuchus) (2nd, 3rd, 5th, 6th, 8th, and 10th hypothesis). Similarly, we find the data trends only for one of the two scheming hetaerae (meretrices callidae), Phronesium (Truculentus) (2nd, 3rd, 5th, 6th, 8th, and 10th hypothesis). The data profile does not apply to the scheming parasites (parasiti callidi).
Overall, we cannot confirm the data profile for all types of scheming characters other than male and female slaves. Therefore, it seems to be closely linked to the character of the scheming slave.
5.3 Scheming Protagonists?
Considering the study of Fischer et al. 2018, the question might arise whether the data profile of the scheming slaves is similar to that of protagonists. It should be noted that many of the schemers are also the protagonists in the respective drama. Since Fischer et al. did not consider the clustering coefficient or the number of triangles in their analysis, it might be interesting to check these measures for other protagonists than the scheming slaves. This way, the data profile of both the schemers and the protagonists could be further sharpened.
5.4 Perspectives
As shown, it has been possible to develop a data profile for a character type in Roman comedy using the method of network analysis and to refine this profile by using count-based measures. Similarly, other digital methods could be used to extend and sharpen this data profile, such as type-focused stylometry. Furthermore, it would be beneficial to ascertain whether the data trends described would also be observed for character types other than scheming slaves. Therefore, it might be interesting to carry out cross-checks. For example, one could check all the slaves in Roman comedy for the data trends, or one could check all the characters in the three comedies that do not feature intrigue for the data profile. These steps would test and improve the developed data profile.
6. Conclusion
The employment of digital methods has opened up a new perspective on the character type of the servus callidus in Roman comedy. Through network analysis, the social capital of the scheming slave has been quantified, thereby enabling a new approach to analysing his position within the group of the dramatis personae, and encompassing all extant Roman comedies. The analysis has also highlighted the characteristic position of the scheming slave in the dramatic network in contrast to other scheming characters. The significant amount of social capital acquired by the servus callidus and his status as a slave present a striking paradox. This observation, thus, complements the studies on how the intrigues of the servus callidus overturn social hierarchies in Roman comedy in a carnivalesque manner. Concurrently, this study demonstrates the potential of digital methods for subject-specific research questions and relatively limited datasets. Roman comedy proved to be an appropriate use case as it draws upon typical motifs and stock characters, resulting in a similar dramatic structure which can be analysed digitally. This study has therefore revealed another facet of both the servus callidus and literary network analysis.
7. Data Availability
Data can be found here: https://github.com/juliajbeine/The-schemer-unmasked and in Beine 2024b / https://doi.org/10.5281/zenodo.10960182.
8. Acknowledgements
This article was written and revised during my affiliations with the Institute of Classical Philology at the Ruhr University Bochum, the Digital Humanities Center at the University Library Bochum, and the Institute of Greek and Latin Languages and Literatures at the Free University Berlin.
I would like to thank my colleagues in the DraCor team for their advice and support on this project. Regarding the processing in R, I would like to thank Ivan Pozdniakov for his tips and advice. Special thanks to Sabina Polesch and Raphaela Eggers for their proofreading and helpful comments on the manuscript. Furthermore, I would like to thank the anonymous reviewers for their constructive feedback.
Parts of this article are based on my dissertation project Das doppelte Spiel des servus callidus. Eine poetologische und gesellschaftliche Reflexionsfigur auf den europäischen Bühnen der Frühen Neuzeit. I received funding for this project from the “Stiftung Bildung und Wissenschaft” and from the “Studienstiftung des deutschen Volkes”. Moreover, I completed a research stay at the Huygens Institute for the History of the Netherlands (Amsterdam) for my dissertation project which was funded by “Erasmus+” and “PR.INT” (Ruhr University Bochum). In this context, I would like to thank the TransLatin team at Huygens ING for their support, particularly Andrea Peverelli who provided insightful feedback on my manuscript. Special thanks also go to Björn Ross and Frank Fischer for commenting on the chapter of my dissertation that presents my network analyses and for sharing their expertise on this method with me.
9. Author Contributions
Julia Jennifer Beine: Conceptualization, Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing.
Notes
- Fuhse defines a social network as follows: “Ein soziales Netzwerk steht für das Muster an Sozialbeziehungen zwischen einer Menge von Akteuren. Sozialbeziehungen bezeichnen beobachtbare Regelmäßigkeiten der Interaktion zwischen Akteuren und entsprechende Verhaltenserwartungen.” (Fuhse 2018, 14). On the theoretical issues that arise when using social network analysis to study dramatic texts, see Trilcke 2013, 203–08, 222–24. Several studies have demonstrated that social network analysis can provide new insights into dramatic texts. For instance, Trilcke et al. trace the phenomenon of small-world networks in German drama (Trilcke 2023, Trilcke et al. 2024). [^]
- On this dependency in general, see Jansen and Diaz-Bone 2011, 75. [^]
- For a discussion of Bourdieu’s concept of social capital in the context of Roman comedy, see Beine 2024a, chapter “Einleitung”. [^]
- For research trends, see Fuhse 2018, 179–83. [^]
- To date, there is no consensus on the definition of centrality nor on the definition of importance of a social actor which results in different approaches and centrality measures. On this theoretical gap, see Mutschke 2010, 365–66, 375–76. [^]
- For the mathematical formula, see Mutschke 2010, 367–68; NetworkX Developers 2023. [^]
- There are different formulae to calculate the betweenness centrality, see Mutschke 2010, 370. This analysis uses the algorithm proposed by Brandes 2001. For further details, see subsection 3.2 of this article. [^]
- For an explanation of the network measures accompanied by examples from Plautus’ Pseudolus, see the glossary in Beine 2024a, chapter “Glossar zur Netzwerkanalyse”. [^]
- Fuhse describes the position of ‘the laughing third’ as follows: “Akteure mit Beziehungen zu ansonsten unverbundenen Akteuren oder Gruppen können diese gegeneinander ausspielen” (Fuhse 2018, 167, cf. 22). In fact, this position can be identified by a low clustering coefficient of a social actor. [^]
- Mutschke emphasises this particularity regarding all structural centrality measures (Mutschke 2010, 373–74). [^]
- Fuhse gives the following definition: “In einem Netzwerk verfügen solche Akteure über Macht, (1) die als Broker zwischen verschiedenen Gruppen fungieren, oder (2) von denen andere Akteure für ihren Zugang zum Netzwerk abhängig sind.” (Fuhse 2018, 168). [^]
- Fuhse lists five network effects: “Zugang zu Informationen”, “Macht”, “Anpassung / sozialer Druck”, “Soziale Kategorisierung”, and “Koordination” (Fuhse 2018, 166–170). [^]
- For an overview of the intrigues in Roman comedy, see the table in Dieterle 1980, 38–42. It shows the aim, means, main schemer, and victim of an intrigue per play and notes whether the scheme is successful respectively. [^]
- For an analysis of these word families, see Beine 2024a, chapter “Das Handwerkszeug der servi callidi”. [^]
- For a detailed discussion of Dieterle’s definition, see Beine 2024a, chapter “Das Handwerkszeug der servi callidi”. [^]
- Note that the network data only captures the participation of characters in the verbal exchange in a scene. It does not evaluate to whom the speech of a character is directed nor the content of the speech. For a detailed discussion, see Beine 2024a, chapter “Einleitung”. [^]
- On this limitation in general, also see Trilcke 2013, 224. [^]
- See also Dieterle 1980, 33, 35. For a comparison of the two slaves to the other servi callidi, see Beine 2024a, chapter “Die antiken servi callidi und materielles Kapital”. [^]
- In Terence’s Hecyra, the young woman Philumena was raped and became pregnant before her marriage. She tries to conceal her pregnancy from her spouse and his relatives by giving false excuses for staying at her mother’s house. Whether this strategy can be considered an intrigue seems debatable (see also Dieterle 1980, 35–36). However, Philumena is not captured in the network analysis as she does not appear on stage and her excuses are solely conveyed through other characters. [^]
- I chose the approach of ranking the network values of the scheming characters to explore whether they have one of the most advantageous positions in the dramatic network compared to the other characters. This approach proves suitable for analysing the scheming characters in Roman comedy, given the relatively small dataset. Alternatively, the network values could be evaluated using percentiles. However, a ranking-based evaluation is more understandable and easier to follow for readers who are less familiar with statistics. The same applies to the evaluation of the count-based values. [^]
- The exact number of slaves in the Aulularia and how to distinguish them from each other is disputed due to partially uncertain and incomplete textual transmission as well as inconsistencies in the conception of the characters. The slave who attempts to buy his freedom with stolen money is referred to as Strobilus by Leo (Plautus 1895–1896), while Lindsay refers to him as a nameless slave of Lyconides (servus Lyconidis, Plautus 1903–1905). The network analysis is based on Leo’s edition. For a discussion on the slaves in the Aulularia, see Stockert 1983, 16–18. [^]
- For a comparative analysis of the social capital of the scheming slaves (servi callidi) with that of their owners and their targets, using network analysis, see Beine 2024a, chapter “Die antiken servi callidi und materielles Kapital”. [^]
References
Beine, Julia Jennifer (2024a). Das doppelte Spiel des servus callidus: Eine poetologische und gesellschaftliche Reflexionsfigur auf den europäischen Bühnen der Frühen Neuzeit. (Bochum, Univ., Diss., 2023). Studia Comica. Verlag Antike. Forthcoming.
Beine, Julia Jennifer (2024b). The Schemer Unmasked. Sketching a Digital Profile of the Scheming Slave in Roman Comedy (v1.0.0) [Data set]. http://doi.org/10.5281/zenodo.10960182.
Beine, Julia Jennifer and Frank Fischer, eds. (2023). Roman Drama Corpus (RomDraCor) (version of Nov. 29, 2023). https://dracor.org/rom (visited on 11/29/2023).
Börner, Ingo and Peer Trilcke (2023). D7.1. On Programmable Corpora. Report and Prototype (DraCor). v1.0.0. http://doi.org/10.5281/zenodo.7664964.
Bourdieu, Pierre (1986). “The Forms of Capital”. In: Handbook of Theory and Research for the Sociology of Education. Ed. by John G. Richardson. Greenwood Press, 241–258.
Brandes, Ulrik (2001). “A Faster Algorithm for Betweenness Centrality”. In: The Journal of Mathematical Sociology 25 (2), 163–177. http://doi.org/10.1080/0022250X.2001.9990249.
Csárdi, Gábor, Tamás Nepusz, Kirill Müller, Szabolcs Horvát, Vincent Traag, Fabio Zanini, and Daniel Noom (2023). igraph for R: R interface of the igraph library for graph theory and network analysis. http://doi.org/10.5281/ZENODO.7682609.
Dieterle, Arnulf (1980). Die Strukturelemente der Intrige in der griechisch-römischen Komödie. Heuremata 6. Grüner.
DraCor (2023). DraCor API: Version 0.91.1. status: beta. eXist-db: 6.0.1. https://github.com/dracor-org/dracor-api/releases/tag/v0.91.1 (visited on 11/29/2023).
Fischer, Frank, Ingo Börner, Mathias Göbel, Angelika Hechtl, Christopher Kittel, Carsten Milling, and Peer Trilcke (2019). “Programmable Corpora: Introducing DraCor, an Infrastructure for the Research on European Drama”. In: Book of Abstracts of the Digital Humanities Conference 2019. ADHO. http://doi.org/10.5281/zenodo.4284002.
Fischer, Frank, Peer Trilcke, Christopher Kittel, Carsten Milling, and Daniil Skorinkin (2018). “To Catch a Protagonist: Quantitative Dominance Relations in German-Language Drama (1730–1930)”. In: Book of Abstracts of the Digital Humanities Conference 2018: Puentes/Bridges. ADHO, 193–201. https://dh2018.adho.org/wp-content/uploads/2018/06/dh2018_abstracts.pdf (visited on 05/31/2023).
Fuhse, Jan Arendt (2018). Soziale Netzwerke: Konzepte und Forschungsmethoden. 2nd ed. UVK Verlag.
Hagberg, Aric A., Daniel A. Schult, and Pieter J. Swart (2008). “Exploring Network Structure, Dynamics, and Function Using NetworkX”. In: Proceedings of the 7th Python in Science Conference (SciPy2008). Ed. by Gäel Varoquaux, Travis Vaught, and Jarrod Millman, 11–15. https://conference.scipy.org/proceedings/SciPy2008/SciPy2008_proceedings.pdf (visited on 05/31/2023).
Iannone, Rich, Joe Cheng, Barret Schloerke, Ellis Hughes, Alexandra Lauer, JooYoung Seo, and Ken Brevoort (2023). gt: Easily Create Presentation-Ready Display Tables. https://gt.rstudio.com/ (visited on 05/31/2023).
Jansen, Dorothea and Rainer Diaz-Bone (2011). “Netzwerkstrukturen als soziales Kapital: Konzepte und Methoden zur Analyse struktureller Einbettung”. In: Soziale Netzwerke. Ed. by Joh. Weyer. Oldenbourg, 71–108. http://doi.org/10.1524/9783486709667.71.
Mutschke, Peter (2010). “Zentralitäts- und Prestigemaße”. In: Handbuch Netzwerkforschung. Ed. by Christian Stegbauer and Roger Häußling. VS Verlag für Sozialwissenschaften, 365–378. http://doi.org/10.1007/978–3–531–92575–2_33.
NetworkX Developers (2023). “closeness_centrality”. In: NetworkX. Documentation. https://networkx.org/documentation/stable/reference/algorithms/generated/networkx.algorithms.centrality.closeness_centrality.html (visited on 05/31/2023).
Neuwirth, Erich (2022). RColorBrewer: ColorBrewer Palettes: Version 1.1–3. https://cran.r-project.org/web/packages/RColorBrewer/index.html (visited on 05/31/2023).
Pedersen, Thomas (2022). ggraph: An Implementation of Grammar of Graphics for Graphs and Networks. https://ggraph.data-imaginist.com (visited on 05/31/2023).
Pfister, Manfred (2001). Das Drama: Theorie und Analyse. 11th ed. Wilhelm Fink. Plautus (1895–1896). Comoediae. Ed. by Fridericus Leo. 2 vols. Weidmann.
Pfister, Manfred (1903–1905). Comoediae. Ed. by Wallace M. Lindsay. Repr. 2004–2006. 2 vols. Scriptorum Classicorum Bibliotheca Oxoniensis. Clarendon.
Pozdniakov, Ivan and Frank Fischer (2023). rdracor: Version 0.7.7. https://github.com/dracor-org/rdracor (visited on 11/29/2023).
R Core Team (2023). R. A Language and Environment for Statistical Computing: Version 4.3.2. Windows 10 x64. https://www.R-project.org (visited on 11/29/2023).
Stockert, Walter (1983). “Einleitung”. In: Aulularia. Ed. by Walter Stockert. Griechische und lateinische Schriftsteller. Teubner, 1–31.
Terence (1857). Comoediae sex. Bibliotheca Classica. Whittaker and Bell.
Trilcke, Peer (2013). “Social Network Analysis (SNA) als Methode einer textempirischen Literaturwissenschaft”. In: Empirie in der Literaturwissenschaft. Ed. by Philip Ajouri, Katja Mellmann, and Christoph Rauen. Poetogenesis. Mentis, 201–247. http://doi.org/10.30965/9783957439710_012.
Trilcke, Peer (2023). “Small Worlds, Beat Charts und die Netzwerkanalyse dramatischer Texte: Reflexionen aus dem Rabbit Hole”. In: Digitale Literaturwissenschaft. Ed. by Fotis Jannidis. Germanistische Symposien. J.B. Metzler, 563–596. http://doi.org/10.1007/978-3-476-05886-7_23.
Trilcke, Peer, Evgeniya Ustinova, Ingo Börner, Frank Fischer, and Carsten Milling (2024). “Detecting Small Worlds in a Corpus of Thousands of Theatre Plays: A DraCor Study in Comparative Literary Network Analysis”. In: Computational Drama Analysis. Ed. by Melanie Andresen and Nils Reiter. De Gruyter. Forthcoming.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy McGowan, Romain François, Garrett Grolemund, Alex Hayes, Lionel Henry, Jim Hester, Max Kuhn, Thomas Pedersen, Evan Miller, Stephan Bache, Kirill Müller, Jeroen Ooms, David Robinson, Dana Seidel, Vitalie Spinu, Kohske Takahashi, Davis Vaughan, Claus Wilke, Kara Woo, and Hiroaki Yutani (2019). “Welcome to the Tidyverse”. In: Journal of Open Source Software 4 (43), 1686. http://doi.org/10.21105/joss.01686.